从试验试错到仿真优化：模态分析如何降低振动测试成本？

模态测试分析可以帮助用户评价现有结构的动态特性、控制结构的辐射噪声、降低产品的噪声水平，并找到振动噪声产生的根源(如消除部件的开裂问题)，以及进行结构动力学修改、产品优化设计、验证有限元模型、提高数字模型的精度。

通常模态分为试验模态分析和工作模态分析。试验模态分析时激励力和响应同时测量， 而工作模态只测试响应，激励力无法测量或不可预知。新能源汽车为提升续航能力，采用"以塑代钢"轻量化设计，这对零部件结构提出更高要求。模态测试技术可精准分析结构动态特性，优化轻量化设计，提升产品性能与可靠性，助力续航突破。

目前，国高材分析测试中心拥有多套振动试验系统，在进行零件前期验证时，有时会出现零件失效状况，试验失效后，客户会修改结构，然后再进行试验，整个过程试验成本投入较高，并且试验周期拉长。国高材分析测试中心能够实现振动领域的CAE基础仿真，有效的识别可能存在缺陷的零部件，优化振动方案，优化结构方案。

在振动实验过程中，对于相同的产品进行不同的固定方式，有时会产生不同的振动效果， 不恰当的固定，会导致零件产生过高的应力，导致其失效，本文将重点借助仿真分析软件，了解其自由和约束状态下的振动试验结果。

2.1 悬臂梁仿真模型

考虑到实际使用的计算机的运行读取速度达不到专业仿真计算机的要求，因而初步以悬 臂梁模型作为研究模型，绘制悬臂梁模型，设计不同弹性系数的弹簧对悬臂梁的一端进行固定，弹簧的刚度范围从接近于零的状态上升到刚度非常大的状态，甚至接近完全约束状态，具体示意图如下图1所示，最上端悬臂梁处于自由状态，理论上其弹性系数为0N/mm³, 最下端悬臂梁处于完全约束状态，理论上 其弹性系数为+∞N/mm³。

图1 悬臂梁的弹簧支承系统

2.2 模态处理方案

在仿真分析软件中对悬臂梁在不同弹簧支承系统下的1~9阶模态进行仿真分析，依次条件弹性系数为 Free、10N/m³、100N/m³、1000N/m³、10000N/m³、100000N/m³、1000000N/m³ 以及趋向于无穷大的固定约束10E+14  N/m³。分别计算悬臂梁在上述固定条件下1~9阶的模态结果，并对不同弹性系数约束条件下的模态结果进行分析与研究，主要关注其振形的变化以及形变量的差异。

3.1 不同约束条件下悬臂梁模态的变化

表1 不同弹性系数约束条件下，1~9阶模态值变化列表

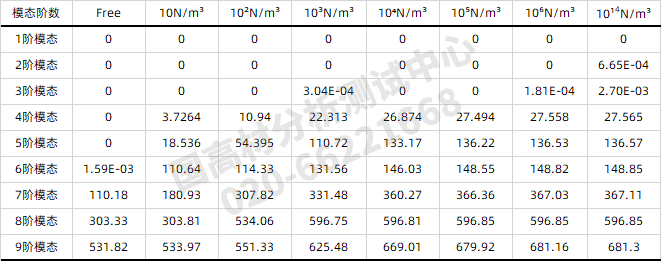
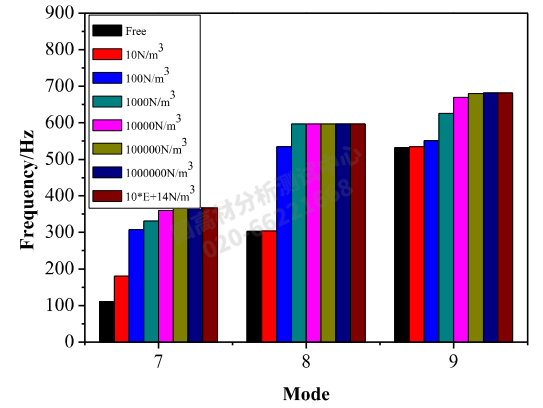
图2 悬臂梁7、8、9阶模态试验结果

从上图2可以看出，随着弹性系数不断的增加，整个悬臂梁振动试验系统刚度分布增加， 根据固有频率的计算公式，其固有频率呈现增加的趋势，尤其是从 Free 状态，到10N/m³, 再到100N/m³，7阶、8阶和9阶模态呈现相对明显的增加趋势。但是当弹性系数再呈现指数级增加时，其对应阶模态频率变化不大，向上增加的频率移动越慢。这是因为结构的共振峰对应的是固有频率，刚度增大后，结构的固有频率会向上移动靠近反共振峰，而反共振峰对应的刚度是无限大的。因此，刚度无限增大，结构的固有频率向上移动不超过反共振峰对应的频率。

3.2 模态阶数随着弹性系数的变化

如下图3所示，当固定约束为 Free状态时，在有限元分析中，计算出来的前6阶模态为刚性模态，这6个模态频率为0或者很小，在欠约束的条件下，悬臂梁的前6阶的振动模 式为刚体运动，可以看成是三个平动方向和三个转动方向的刚体运动的合成。此时悬臂梁结构没有发生弹性变形的现象。

图3 自由状态 (Free) 下1-6阶模态振型

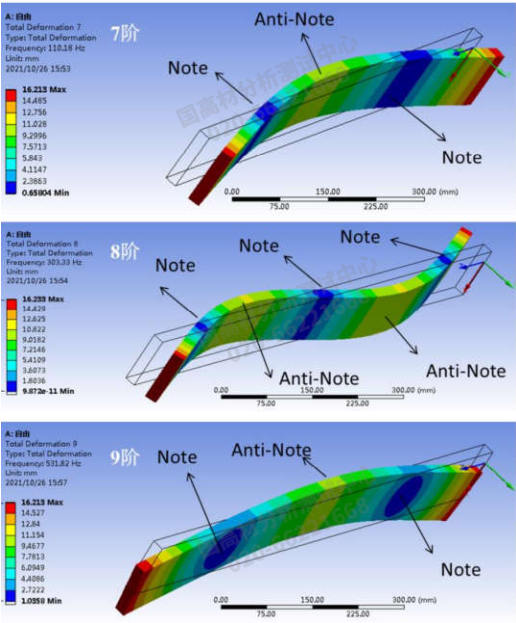
图4 自由状态 (Free) 下7-9阶模态振型

7阶和8阶振型主要是沿着悬臂梁径向方向进行正弦函数振动，7阶振型悬臂梁有2个节点，分别为图4中蓝色位置处，该区域变形量较低，几乎无变形现象，同时有1个反节点， 变形量较大，约为9.8mm，由于悬臂梁处于自由状态，因而其两端的变形量较高约为16.2mm；8阶振型悬臂梁有一个节点，分别为图中蓝色位置处，该区域变形量较低，同时有两个反节点，变形量较大，约为10.6mm，其两端的变形量较高约为16.2mm 。而9阶振型是沿着悬臂梁的横向方向进行正弦函数振动，同样存在2个节点，变形量几乎为0mm，1个反节点， 变形量9.6mm，其两端的变形量较高约为16.2mm。

当弹性系数增加时，仅仅增加10N/mm³ 时，就出现了4阶模态，表明在悬臂梁系统中出现了弹性模态。但是在弹性系数增加的过程中，结构虽然约束质量越来越高，但是仍然属于弹性约束，结构件和约束件之间还存在相对位移，因而此时，系统之间还是会存在刚性模态(1~3阶模态为0或者很小)。

3.3 悬臂梁刚性约束振动规律探究

以约束方式为刚性约束，对悬臂梁的正弦振动和随机振动规律进行探究，分析得其前九阶模态结果如下表2所示。

表2悬臂梁刚性约束模态分析结果(前九阶)

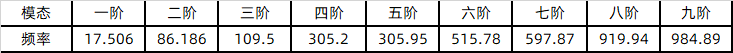
目前对结构的固有频率测试，常见的有两种方式：锤击法和激振器法。由于固有频率是模态的重要参数之一，所以，采用上述两种方法测试需要遵循激励和响应的位置避开模态节点的位置。否则会造成某阶固有频率测试丢失现象。

3.4 悬臂梁锤击法固有频率测试CAE仿真

力锤法作为激励设备，设备简单，投资小。相对振动台激振器而言，力锤移动方便  不影响被测结构的动态特性，对于一些小型的结构件，选择力锤法进行模态测试相对较方便。并且力锤激励属于宽带激励，可根据不同的关心频率的范围，选择不同的锤头。

下面我们主要以上述模态研究部分的悬臂梁结构为模型，进行力锤法测试模态的影响因数研究。

图5 固定约束施加激励信号，试验结果图

如上图5所示，当选择在固定约束处施加1000N 的激励信号，悬臂梁样品没有发生振动现象，对于监测位置点的频率响应没有产生任何响应，振幅和相位角分别保持在0m/s² 和0，表明悬臂梁样品没有发生任何激励现象。因而在实际试验时，对于 力锤的激励需要避免在刚性固定处施加激励信号，同时在前面也提到过，激励信号需要避开模态节点的位置，尤其是我们关心低阶模态的位置，如果在某低阶模态的节点位置施加激励 信 号 ， 那 么 该 阶 模 态 的 响 应 将 不 能 测 试 到 。

直接对悬臂梁施加三方向的激励，观察上述同样的悬臂梁端点的频率响应(对 该端点X、Y和 Z 方向均施加1000N 激励)。试验结果如下：

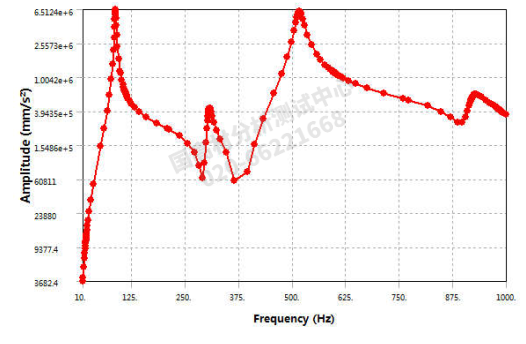
图6 悬臂梁端点X 向加速度信号监测结果图(三方向施加激励)

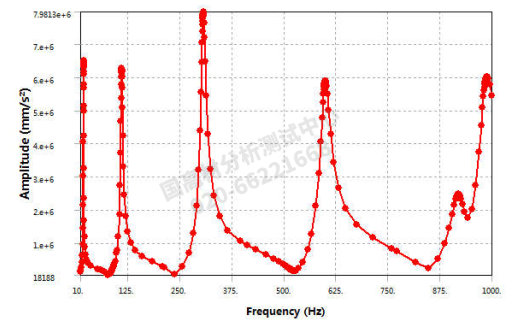
图7 悬臂梁端点Y 向加速度信号监测结果图(三方向施加激励)

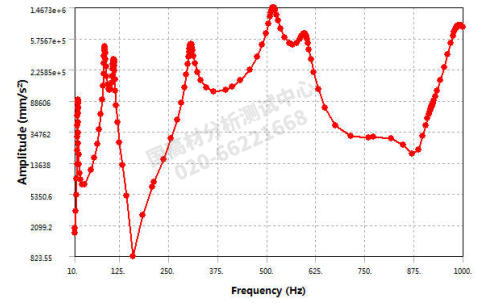
图8 悬臂梁端点Z 向加速度信号监测结果图(三方向施加激励)

从上图6~8可以看出，当施加三方向的施加激励时，出现更多的模态信号，具体频率结果如下表4所示。从表中可以看出，悬臂梁端点Z 向加速度监测信号多了86.107Hz 以及 515.57Hz, 这个如上图 3所示，正好是悬臂梁沿着其横向强振动方向的模态频率。但是三方向的激励方式还是没有监测到扭转振动的激励频率。

表3 三方向力激励下，悬臂梁端点Z 向加速度信号监测结果表

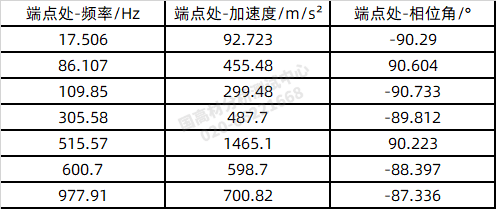
综上，在实际力锤试验测试固有频率过程中，需要注意如下注意事项：

1、施加激励(力锤敲击处)，以及添加响应(添加加速度计)的位置应该避免靠近刚性较强的区域，以及避开某关心的低阶模态的节点处。

2、如果只是单方向施加激励，会监测不到强方向性振动以及扭转振动振型的模态频率，采用多方向的激励信号可以测试(即力锤沿着样品的不同方向进行敲击)，将会测量得到相 对较全的横向振动和径向振动振型的模态。